| 游牧小说网 同人小说 言情小说 竞技小说 架空小说 乡村小说 都市小说 网游小说 科幻小说 仙侠小说 官场小说 耽美小说 军事小说 |
| 小说排行榜 穿越小说 玄幻小说 历史小说 校园小说 总裁小说 综合其它 武侠小说 重生小说 推理小说 经典名著 灵异小说 短篇文学 |
| 好看的小说 公关生涯 情在商场 美腿妈妈 红杏出墙 亲妈后妈 七年之痒 远山呼唤 女人如烟 小镇风月 奶孙乱情 热门小说 全本小说 |
|
更多与明史小说免费阅读相关的优秀历史小说请收藏游牧小说网
|
|
|
|
| 游牧小说网 > 历史小说 > 明史 作者:张廷玉等 | 书号:10209 时间:2017/3/26 字数:11088 |
| 上一章 章八 下一章 ( → ) | |
| 历二 ▲大统历法一上(法原) 造历者各有本原，史宜备录，使后世有以考。如《太初》之起数钟律，《大衍》之造端蓍策，皆详本志。《授时历》以测算术为宗，惟求合天，不牵合律吕、卦爻。然其法所以立，数之所从出，以及晷影、星度，皆有全书。郭守敬、齐履谦传中，有书名可考。《元史》漫无采摭，仅存李谦之《议禄》、《历经》之初稿。其后改三应率及立成之数，与夫割圆弧矢之法，平立定三差之原，尽削不载。使作者精意湮没，识者憾焉。今据《大统因通轨》及《历草》诸书，稍为编次，首法原，次立成，次推步。而法原之目七：曰句股测望，曰弧矢割圆，曰⻩⾚道內外度，曰⽩道  周，曰⽇月五星平立定三差，曰里差刻漏。▲句股测望 京北立四丈表，冬至⽇午正，测得景辰七丈九尺八寸五分。随以简仪测到太  南至地平二十六度四十六分半，为半弧背。求得矢度，五度九十一分半。置周天半径，截矢余五十四度九十六分为股，乃本地支戴⽇下之度。以弦股别句术，求得句二十六度一下七分六十六秒，为⽇出地半弧弦。京北立四丈表，夏至⽇午正，测得景长一丈一尺七寸一分。随以简仪测到太 南至地平七十四度二十六分半，为半弧背。求得矢度，四十三度七十四分少。置周天半径，截矢余一十七度一十三分二十五秒为句，乃本地去戴⽇下之度。以句弦别股术，求得股五十八度四十五分半，为⽇出地半弧弦。以二至⽇度相并，得一百度七十三分，折半得五十度三十六分半，为京北⾚道出地度。以⾚道出地度转减周天四之一，余四十度九十四分九十三秒七十五微，为京北北极出地度。 ▲弧矢割圆 周天经一百二十一度七十五分少。(少不用。)半径六十零度八十七分半。(又为⻩⾚道大弦。)二至⻩⾚道內外半弧背二十四度。(所测就整。)二至⻩⾚道弧矢四度八十四分十二秒。⻩⾚道大句二十三度八十分七十秒。⻩⾚道大股五十六度零二分六十八秒。(半径內减去矢度之数。) 割圆求矢术 置半弧度自之，为半弧背幕，周天径自之，为上廉。上廉乘半弧背幕，为正实。上廉乘径，为益从方。半弧背倍之，乘径，为下廉。以初商乘上廉，得数以减益从方，余为从方。置初商自之以下廉，余以初商乘之，为从廉。从方、从廉相并，为下法。下法乘初商，以减正实，实不⾜减，改初商。实有不尽，次第商除之。倍初商数，与次商相并以乘上廉，得数以减益从方，余为从方。并初商次商而自之，又以初商自之，并二数以减下廉，余以初商倍数并次商乘之，为从廉。从方、从廉相并，为下法。下法乘次商，以减余实，而定次商。有不尽者，如法商之，皆以商得数为矢度之数。(⻩⾚道同用。) 如以半弧背一度求矢。术曰：置半弧背一度自之，得一度，为半弧幕。置周天径一百二十一度太自之，得一万四千八百二十三度零六分二十五秒，为上廉。上廉乘半弧背幕，得一万四千八百二十三度零六分二五，为正实。上廉又乘径，得一百八十零万四千七百零七度八十五分九十三秒七五，为益从方。半弧背一度倍之，得二度，以乘径得二百四十三度五十分，为下廉。初商八十秒。置初商八十秒乘上廉一万四千八百二十三度零六二五，得一百一十八度五八四五，以减益从方一百八十零万四千七百零七度八五九三七五，余一百八十零万四千五百八十九度二七四八七五，为从方。又置初商八十秒自之，得六十四微，以减下廉余二百四十三度四九九三六。仍以八十秒乘之，得一度九四七九九九四八八，为从廉。以从廉、从方并之，共得一百八十零万四千五百九十一度二二二八七四四八八，为下法。下法乘初商，得一万四千四百三十六度七十二分九七八二九九五九零四，以减正实，余实三百八十六度三十三分二七一七零零四零九六。次商二秒。置初商八十秒倍之，得一分六十秒。加次商二委六十二秒，乘上廉一万四千八百二十三度零六二五，得二百四十零度一三三六一二五，以减益从方，余一百八十零万四千四百六十七二五七六二五，为从方。又置初次商八十二秒自之，得六十七微。加初商八十秒自之之数，得一秒三十一微，以减下廉，余二百四十三度四九九八六九。以前所得一分六十二秒乘之，得三度九十四分四六九七八七七八，为从廉。以从廉、从方并，得一百八十零万四千四百七十一度六十七分零四六零三七八，为下法。下法乘次商，得三百六十零度八九四三三四零九二零七五五六，以减余实，仍余二十五度四三八三八二九一二零二零四四。(不⾜一秒叶不用，下同。) 凡求得矢度八十二秒，余度各如上法，求到矢度，以为⻩⾚相求及其內外度之 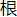 。(数详后。)▲⻩⾚道差 求⻩⾚道各度下⾚道积度术。 置周天半径內减去⻩道矢度，余为⻩⾚道小弦。置⻩⾚道小弦，以⻩⾚道大股乘之(大股见割圆)为实。⻩⾚道大弦(半径)为法。实如法而一，为⻩⾚道小股。直⻩道矢自乘为实，以周天全径为法，实如法而一，为⻩道半背弦差。以差去减⻩⾚道积度，(即⻩道半弧背。)余为⻩道半弧弦。置⻩⾚道半弧弦自之为股幕，⻩⾚道小股自之为句幕，二幕并之，以开平方法除之，为⾚道小弦。置⻩⾚道半弧弦，以周天半径(亦为⾚道大弦)乘之为实，以⾚道小弦为法而一，为⾚道半弧弦。置⻩⾚道小股，(亦为⾚道横小句)以⾚道大弦(即半径)乘之为实，以⾚道小弦为法而一，为⾚道横大句，以减半径，余为⾚道磺弧矢。横弧矢自之为实，以全径为法而一，为⾚道半背弦差。以差加⾚道半弧，为⾚道积度。 如⻩道半弧背一度，求⾚道积度。术曰：“置半径六十零度八十七分五十秒，(即⻩⾚道大弦。)內减⻩道矢八十二秒余六十零度八六六八，为⻩⾚道小弦。置⻩⾚道小弦，以⻩⾚道大股五十六度零二六八乘之，得三千四百一十零度一七二零三零二四为实，以⻩⾚道大弦六十零度八七五为法，实如法而一，得五十六度零一分九十二秒，为⻩⾚道小股。(又为⾚道小句。)置矢度八十二秒自之，得六十七微，以全径一百二十一度七五为法，除之得五十五纤，为⻩道平半背弦差。置⻩道半弧弦一度，內减⻩道半背弦差，余为半弧弦，因因差在微以下不减，即用一度为半弧弦。置⻩道半弧弦一度自之，得一度为股幕。⻩⾚道小股五十六度零一矣二自之，得三千一百三十八度一五零七六八四六为句幕。二幕并得三千一百三十九度一五零七六八四六为弦实，平方开之，得五十六度零二八一，为⾚道小弦。置⻩道半弧弦一度，以半径(即⾚道大弦)乘之，得六十零度八七五为实，以⾚道小股五十六度零二八一为法除之，得一度零八分六十五秒，为⾚道半弧弦。置⻩⾚道小股五十六度零一九二，(又为⾚道小句。)以⾚道大弦(半径)六十零度八七五乘之，得三千四百一十零度一六八八为实，以⾚道小弦为法除之，得六十零度八十六分五十三秒，为⾚道横大句。置半径六十零度八十七分五十秒，內减⾚道大句六十零度八十六分五十三秒，余九十七秒，为⾚道横弧矢。置⾚道横弧矢九十七秒自之，得九十四微零九，以全径为法除之，得七十纤，为⾚道背弦差。置⾚道半弧弦一度零八分六十五秒，加⾚道背弦差，为⾚道积度，今差在微已下不加，即用半弧弦为积度。 凡求得⾚道积度一度零八分六十五秒。余度各如上法，求到各⻩道度下⾚道积，两数相减，即得⻩⾚道差，乃至后之率。其分后，以⾚道度求⻩道，反此求之，其数并同。 ▲⻩⾚道相求弧矢诸率立成上 (表格略) ▲⻩⾚道相求弧矢诸率立成下 (表格略) 按郭敬创法五端，內一曰⻩道差，此其 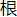率也。旧法以一百一度相减乘。《授时》立术，以句股、弧矢、方圆、斜直所容，求其数差，合于浑象之理，视古为密。顾《至元历经》所载略，又误以⻩道矢度为积差，⻩道矢差为率，今正之。▲割圆弧矢图 凡浑圆中剖，则成平圆。任割平圆之一分，成弧矢形，皆有弧背，有弧弦，有矢。剖弧矢形而半之，则有半弧背，有半弧弦，有矢。因弦矢句股形，以半弧弦为句，矢减半径之余为股，半径为弦。句股內成小句股，则有小句、小股、小弦、而大小可互求，平侧可互用，浑圆之理，斯为密近。 平者为⾚道，斜者为⻩道。因二至⻩道⾚之距，生大句股。因各度⻩⾚之距，生小句股。 外大圆为⾚道。从北极平视，则⻩道在⾚道內，有⾚道各度，即各有其半弧弦，以生大名股。又各有其相当之⻩道半弧弦，以生小句股。此二者皆可互求。 按旧史无图，然表亦图之属也。今句股割弧矢之法，实为历家测算之本。非图不明，因存其要者数端。 ▲⻩⾚道內外度 推⻩道各度，距⾚道內外及去极远近术。置半径內减去⾚道小弦，余为⾚道二弦差。(又为⻩⾚道小弧矢，又为內外矢，又为股弦差。)置半径內外减去⻩道矢度，余为⻩⾚道小弦，以二至⻩⾚道內外半弧弦乘之为实，以⻩⾚道大弦为法，(即半径。)除之为⻩⾚道小弧弦。(即⻩⾚道內外半弧弦，又为⻩⾚道小句。)置⻩⾚道小弧矢自之，(即⾚道二弦差。)以全径除之，为半背弦差。以差加⻩⾚道小弧弦为⻩⾚道小弧半背，即⻩⾚道內外度。置⻩⾚道內外度，视在盈初缩末限以加，在缩初盈天限以减，皆加减象限度，即各得太 去北极度分。如冬至后四十四度，求太 去⾚道內外及去极度。术曰：“置半径六十零度八十七分半，內减⻩道四十四度下⾚道小弦五十八度三十五分六十九秒，余二度五十一分八十一秒，为⻩⾚道小弧矢。(即內外矢。)置半径六十零度八七五，內减⻩道四十四度，矢一十六度五十六分八十二秒，余四十四三十零分六十八秒，为⻩⾚道小弦。置⻩⾚道小弦，以二至⻩⾚道內外半弧弦二十三度七十一分乘之，得一千零五十零度五十一分四二三八为实，以⻩⾚道大弦六十零度八七五为法除之，得一十七度二十五分十九秒为⻩⾚道小弧弦。(即內外半弧弦。)置⻩⾚道小弧矢二度五十一分八十一秒自之为实，以全径地百二十一度七十五分除之，得五分二十一秒为背弦差，以差加⻩⾚道小弧弦一十七度二十五分六十九秒，得一十七度三十零分八十九秒，为二至前后四十四度，太去⾚道內外度。置象限九十一度三十一分四十三秒七五，以內外度一十七度三零八九加之，得一百零八度六十二分三十二秒七五，为冬至后四十四度太去北极度。▲⻩道每度去⾚道內外及去北极立成 (表格略) ▲⽩道 周推⽩⾚道正 ，距⻩⾚道正北极数。术曰：“置实测⽩道出⼊⻩道內外六度为半径弧弦，又为大图弧矢，又为股弦差。置半径六十零度七五自之，得三千七百零五度七六五六二五，以矢六度而一，得六百一十七度六十三分为股弦和，加矢六度，共六百二十三度六十三分为大圆径。依法求得容阔五度七十分，又为小句。又以二至出⼊半弧弦二十三度七十一分为大句。以大句为法，除大股五十六度零六分五十秒，得二度三十七分(就整)为度差。以度差乘小句，得小股一十三度四十七分八十二秒，为容半长。置半径六十零度八七五为大弦，以乘小句五度七十分为实，以大句二十三度七十一分为法除之，得一十四度六十三分为小弦，又为⽩⾚道正，距⻩⾚道正半弧弦。 依法求行半弧背一十四度六十六分，为⽩⾚道正距⻩⾚道正极娄数。译文 制定历法的人各有自己的渊源，史书应该详尽采录，使后世有参考的依据。 如《太初历》起源于音律，《大衍历》发端于蓍卜，都详细见于本历志。 《授时历》以测量检骏推算焉宗旨，祇求与天相合，不牵強附会音律、卦爻。 然而它立法的依据．数据的出处，以及⽇晷影长、行星度数，都有完整的书籍。 郭守堃、查履谦的传中，有书名可考。 《元史》全没有采录，现仅存奎盏的《议录》、《历经》的初稿。 后来改变三应率及数据表的数据，和割圆弧矢的方法、平立定三差的来源，都删去没有记载。 使作者的精辟见解湮汝无闻，有见识的人都为此感到道憾。 现在 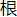据《大统历通轨》及《历草》等书，稍加编排，首先是历法原理，其次是数据表，再其次是推算。而历法原理的细目有七项，是勾股测望，弧矢割圆，⻩⾚道差，⻩⾚道內外度，⽩道 周，⽇月五星平立定三差，里差刻漏。在京北立四丈⾼的标尺，冬至⽇正午，测得影长七丈九尺八寸五分。 随即用简仪测得太 南至地平二十六度四十六分半，焉半弧背。求得矢度为五度九十一分半。 将周天半径，减去矢度，剩余五十四度九十六分为股，就是本地离头顶上太 的度数。用以弦股求勾的方法，求得勾为二十六度十七分六十六秒，就是太 出地的半弧弦。在京北立四丈⾼的标尺，夏至⽇正午，测得影长一丈一尺七寸一分。 随即用简仪测到太 南至地平七十四度二十六分半，为半弧背。求得矢度为四十三度七十四分又四分之一。 将周天半径，减去矢度，剩下十七度十三分二十五秒焉勾，就是本地离头顶上太 的度数。用以勾弦求股的方法，求得股为五十八度四十五分半，就是太 出地的半弧弦。将冬至夏至太 南至地平的度数相加，得一百度七十三分，折半得五十度三十六分半，为京北的⾚道出地度数。以⾚道出地度转减周天的四分之一，余四十度九十四分九十三秒七十五微，就是京北的纬度。 周天圆的直径为一百二十一度七十五分又四分之一。 四分之一不用。 半径为六十度八十七分半。 又是⻩道⾚道的大弦。 冬至夏至⻩道⾚道內外半弧背为二十四度。 所测敷取整数。 冬至夏至⻩道⾚道弧矢为四度八十四分八十二秒。 ⻩道⾚道大勾为二十三度八十分七十秒。 ⻩道 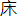 道大股为五十六度零二分六十八秒。半径內减去矢度。 割圆求矢的方法。 将半弧背的度数自乘，就是半弧背的幂。 将周天圆的直径自乘，就是上廉。 上廉乘半弧背的幂，就是正实。 上廉乘以天圆直径，就是益从方。 半弧背乘以二，乘以天圆直径，就是下廉。 用初商乘上廉，再用益从方减去这个得数，余数就是从方。 将初商自乘并用下廉减自乘的得数，余数乘以初商，就是从廉。 从方和从廉相加，就是下法。 下法乘以初商，再用正寅减去此数，如正赏不够减，就改用初商。 正实还有余数，依次用商除下去。 将初商乘以二，与次商相加并乘以上廉，再用益从方减去乘积，余数为从方。 将初商和次商相加并自乘，又将初商自乘，然后两数相加，再用下廉城此数，余数用初商的二倍加次商舆之相乘，就是从廉。 从方和从廉相加，就是下法。 下法乘以次商，再用余实碱此数，从而确定次商。 如还有余数，用同样的方法计算，商的得敷就是矢的度数。 ⻩道⾚道同用这一度数。 例如以半弧背一度来求矢的度数。 方法是：将半弧背一度自乘，得敷为一度，是半弧背的幂。 将天圆直径一百二十一度又四分之三自乘，得一万四千八百二十三度零六分二十五秒，就是上廉。 上廉乘以半弧背的幂，得一万四千八百二十三度零六分二十五秒，就是正实。 上廉又乘天圆直径，得一百八十万四千七百零七度八十五分九十三秒七五，就是益从方。 半弧背一度加倍，得二度，乘以天圆直径得二百四十三度五十分，就是下廉。 初商八十秒。 将初商八十秒乘以上廉一万四千八百二十三度零六二五，得一百一十八度五八四五，再用益从方一百八十万四千七百零七度八五九三七五减此数，余一百八+葛四千五百八十九度二七四八七五，就是从方。 又将初商八十秒自乘，得六十四微，再用下廉减此敷，余二百四十三度四九九九三六。 仍然用八十秒乘此余数，得一度九四七九九九四八八，就是从廉。 将从廉和从方相加，共得一百八十万四千五百九十一度二二二八七四四八八，就是下法。 下法乘以初商，得一万四千四百三十六度七十二分九七八二九九五九零四，再用正实蔵去此数，得余实三百八十六度三十三分二七一七零零四零九六。 次商二秒。 将初商八十秒加倍，得一分六十秒。 加次商二秒，得一分六十二秒，乘以上廉一万四千八百二十三度零六二五，得二百四十度一三三六一二五，再用益从方减此数，余一百八十万四千四百六十七度七二五七六二五，就是从方。 又将初商和次商八十二秒自乘，得六十七微。 加上初商八十秒自乘之数，得一秒三十一微，用下廉减此敷，余二百四十三度四九九八六九。 乘以前面所得到的一分六十二秒，得三度九十四分四六九七八七七八，就是从廉。 将从廉和从方相加，得一百八十万四千四百七十一度六十七分零四六零三七七八，就是下法。 将下法乘以次商，得三百六十度八九四三三四零九二零七五五六，用余实减此敷，还余二十五度四三八三八二九一二零二零四四。 不⾜一秒舍弃不用，以下同。 求得矢的度数共八十二秒，剩余部分继续用上列方法计算。 求得矢的度数，作为⻩道⾚道相求及求二者內外度的 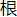。数据详见后文。 求⻩道各度之下⾚道度数的方法。 将天圆的半径减去⻩道矢的度数，余数焉⻩道⾚道的小弦。 将⻩道⾚道的小弦，乘以⻩道⾚道的大股大股见弧矢割圆作为被除数。 ⻩道⾚道的大弦天圆半径作为除数。 两数相除，就是⻩道⾚道的小股。 将⻩道的矢自乘作为被除数，以天圆的直径作为除数，两数相除，就是⻩道半背弦差。 用⻩道积度即⻩道半弧背减这个差，余数就是⻩道半弧弦。 将⻩道半弧弦自乘作为股的幂，⻩道⾚道小股自乘作为勾的幂，两个幂相加，开平方，就是⾚道小弦。 将⻩道的半弧弦，乘以天圆的半径也是⾚道大弦作为被除数，以⾚遒小弦作为除数与之相除，就是⾚道的半弧弦。 将⻩道⾚道的小股，也是⾚道的横小勾。 用⾚道大弦即半径相乘作为被除数，以⾚道小弦作为除数与之相除，就是⾚道横大勾，再用半径减⾚道横大勾，余数就是⾚道横弧矢。 将横弧矢自乘作为被除数，以直径作为除数与之相除，就是⾚道的半背弦差。 以半背弦差加⾚道半弧弦，就是⾚道的度数。 如⻩道半弧背为一度，求⾚道的度数。 方法是：将半径六十度八十七分五十秒，即⻩道⾚道大弦。 ⻩道的矢八十二秒，余六十度八六六八，就是⻩道⾚道小弦。 将⻩道⾚道小弦，乘以⻩道⾚道大股五十六度零二六八，得三千四百一十度一七二零三零二四作为被除数，以⻩道⾚道大弦六十度八七五作为除数，两敷相除，得五十六度零一分九十二秒，就是⻩道⾚道的小股。 又是⾚道小勾。 将矢的度数八十二秒自乘，得六十七微，以天圆直径一百二十一度七五作为除数，舆之相除得五十五纤，就是⻩道半背弦差。 将⻩道半弧背一度，减⻩道半背弦差，余数就是半弧弦。 因半背弦差在一微以下，所以不减，就用一度作为半弧弦。 将⻩道半弧弦一度自乘，得一度作为股的幂。 ⻩道⾚道小股五十六度零一九二自乘，得三千一百三十八度一五零七六八四六作为勾的幂。 两个幂相加得三千一百三十九度一五零七六八四六焉弦实，开平方，得五十六度零二八一，就是⾚道小弦。 将⾚道半弧弦一度，乘以天圆半径，即⾚道大弦。 得六十度八七五作为被除数，以⾚道小弦五十六度零二八一作为除敷相除，得一度零八分六十五秒，就是⾚道的半弧弦。 将⻩道⾚道的小股五十六度零一九二，又是⾚道小勾。 乘以⾚道大弦天圆半径六十度八七五，得三千四百一十度一六八八作为被除数，以⾚道小弦作为除数相除，得六十度八十六分五十三秒，就是⾚道横大勾。 将天圆半径六十度八十七分五十秒，减⾚道大勾六十度八十六分五十三秒，余九十七秒，就是⾚道横弧矢。 将⾚道横弧矢九十七秒自乘，得九十四微零九，再以天圆直径作除数舆之相除，得七十七纤，就是⾚道背弦差。 将⾚道半弧弦一度零八分六十五秒，加⾚道背弦差，就是⾚道的度数。 现在⾚道背弦差在一微以下，舍弃不加，就用半弧弦作为度数。 共求得⾚道度数为一度零八分六十五秒。 其余度数各自用上面的方法，求到各⻩道度数下的⾚道度数，两敷相减，就得到⻩道⾚道差，这是冬至夏至后的比率。 舂分秋分以后，以⾚道度数求⻩道，反过来相求，数据都相同。 按郭守敬创立的新方法有五条，其中一条是⻩道⾚道差，这就是它的数据。 旧方法用一百零一度相减相乘。 《授时历》创立新方法，用勾股、弧矢、方圆、斜直所包含的內容，推求⻩道⾚道的差敷，合乎天象的原理，比古代更严密。 只是《至元历经》的记载很筒略，又误以⻩道矢度为积差，⻩道矢差为差率，现在予以纠正。 凡是圆周从中间剖开，就成了半圆。 任意切分半圆的一部分，就成了弧矢形，都有弧背，有弧弦，有矢。 切分出弧矢形的一半，就有半弧背，有半弧弦，有矢。 因为弦和矢就生出勾股形，以半弧弦焉勾，半径减矢的余数为股，半径为弦。 勾股內又形成小勾股，就有小勾、小股、小弦，而大小可以互相推求，平侧可以互相利用，圆周的道理，这就很切近了。 平线是⾚道，斜线是⻩道。 因为冬至夏至⻩道⾚道的距离，生出大勾股。 因为各度⻩道⾚道的距离，生出小勾股。 外面的大圆是⾚道。 从北极俯视，⻩道在⾚道之內，有⾚道的各度，就有各度的半弧弦，以此生出大勾股。 又各有舆它们相应的⻩道半弧弦，以此生出小勾股。 这二者可以互相推求。 按旧史书没有图，然而表也是和圆同类的。 现在勾股割圆弧矢的方法，实在是历算家测算的 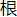本。没有图不能说明问题，因而保留其重要的几幅。 推算⻩道各度距离⾚道的內外度数及距离北极远近的方法。 将天圆半径减去⾚道小弦，余敷就是⾚道两个弦的差。 又是⻩道⾚道小弧的矢，又是內外矢，又是股弦差。 将半径减去⻩道矢的度数，余数就是⻩道⾚道的小弦。 将冬至夏至⻩道⾚道內外半弧弦舆⻩道⾚道小弦相乘作为被除数，以⻩道⾚道大弦作为除数，即半径。 舆之相除就是⻩道⾚道小弧弦。 就是⻩道⾚道內外半弧弦，又是⻩道⾚道小勾。 将⻩道⾚道小弧矢自乘，即⾚道两弦的差。 除以直径，就是半背弦差。 用这个差加⻩道⾚道小弧弦就是⻩道⾚道小弧半背，也就是⻩道在⾚道內外的度数。 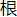据⻩道在⾚道內外的度数，如果在盈初缩末象限表內就加，在缩初盈末象限表內就减，都加减象限表內的度数，就得到太距离北极的度数。如冬至后⻩道四十四度，求太 距离⾚道內外的度数及距离北极的度数。方法是：将天圆半径六十度八十七分半，减⻩道四十四度时⾚道小弦五十八度三十五分六十九秒，余二度五十一分八十一秒，就是⻩道⾚道小弧矢。 即內外矢。 将半径六十度八七分半，减⻩道四十四度时的矢一十六度五十六分八十二秒，余四十四度三十分六十八秒，就是⻩道⾚道小弦。 将⻩道⾚道小弦，用冬至夏至时⻩道⾚道內外半弧弦二十三度七十一分舆之相乘，得一千零五十度五十一分四二三八作为被除数，以⻩道⾚道大弦六十度八七五作为除数舆之相除，得十七度二十五分六十九秒，即⻩道⾚道小弧弦。 即內外半弧弦。 将⻩道⾚道小弧矢二度五十一分八十一秒自乘作为被除数，用直径一百二十一度七十五分与之相除，得五分二十一秒就是背弦差。 用背弦差加⻩道⾚道小弧弦十七度二十五分六十九秒，得十七度三十分八十九秒，就是冬至夏至前后⻩道四十四度时，太 距离⾚道的內外度。将象限九十一度三十一分四十三秒七五，加內外度十七度三零八九，得一百零八度六十二分三十二秒七五，就是冬至后⻩道四十四度时太 距离北极的度数。推算⽩道和⾚道的降 点距离⻩道⾚道降点的最大数值。方法是：将寅测到的⽩道出⼊⻩道內外的六度作为半弧弦，又是大圆的弦矢，又是股和弦的差。 将半径六十度八七五自乘，得三⼲七百零五度七六五六二五，用矢六度与之相除，得六百一十七度六十三分为股弦的和，再加矢六度，共六百二十三度六十三分，就是大圆直径。 按法则求得容阔五度七十分，又是小勾。 又以冬至夏至时出⼊半弧弦二十三度七十一分作为大勾。 以大勾作除数，除大股五十六度零六分五十秒，得二度三十七分就整敷而言为度差。 以度差乘小勾，得小股十三度四十七分八十二秒，就是容半长。 以半径六十度八七五焉大弦，乘以小勾五度七十分作为被除数，以大勾二十三度七十一分焉除数舆之相除，得十四度六十三分就是小弦；又是⽩道⾚道降 点距离⻩道⾚道降点的半弧弦。按法则求得半弧背十四度六十六贫，就是⽩道⾚道降 点距离⻩道⾚道降点的最大敷值。
UｍuXｓ.CoM |
|
| 上一章 明史 下一章 ( → ) |
| 您目前阅读的是明史,历史小说明史小说免费阅读已更新供您免费阅读,非常感谢您对作者张廷玉等的支持,想要阅读更多与明史小说免费阅读类似及相关的优秀历史小说请持续收藏游牧小说网 |